On-Axis Field of a Finite, Straight, Thin Shell Solenoid

This formula uses the formula for the field due to a current loop, integrated over a range of axial displacements to obtain the magnetic field at any point on the axis of a finite, thin shell solenoid.

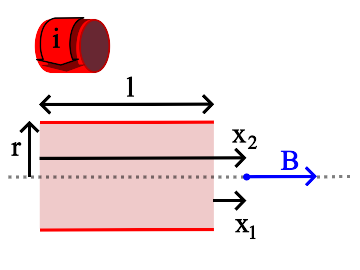
$B = \frac {\mu_o i N}{2 l} \left [ \frac {x_2} {\sqrt{x_2^2 + r^2}} - \frac {x_1} {\sqrt{x_1^2 + r^2}}\right ]$

B is the magnetic field, in teslas, at any point on the axis of the solenoid. The direction of the field is parallel to the solenoid axis.

$\mathbf \mu_o$ is the permeability constant (1.26x10^-6 Hm^-1)

i is the current in the wire, in amperes.

N is the total number of turns of wire in the solenoid.

l is the length of the solenoid, in meters.

r is the radius of the solenoid, in meters.

x₁ and x₂ are the distances, on axis, from the ends of the solenoid to the magnetic field measurement point, in meters.

Special Case: x₁ = -x₂

$B = \frac {\mu_o i N}{\sqrt{l^2 + 4 r^2}}$

The magnetic field measurement point is at the center of the solenoid.

---

Magnet Formulas, © 2018 by Eric Dennison. Source code and License on Github